Effective Axial Modulus
The effective axial modulus is determined from the basic definition of axial modulus. The axial load 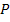 is applied to the composite cylinder. The axial stress is uniform across the cross section. Further, this stress can be given as the axial load divided by the cross sectional area, that is, is applied to the composite cylinder. The axial stress is uniform across the cross section. Further, this stress can be given as the axial load divided by the cross sectional area, that is,
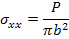 |
(7.186) |
If the effective axial modulus is 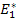 is known then the axial strain can be given as is known then the axial strain can be given as
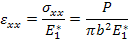 |
(7.187) |
For the axial load applied, the radial stress on the outer boundary, that is, at 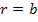 is zero. Thus, is zero. Thus,
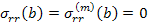 |
(7.188) |
Thus, from the last of Equation (7.185), this becomes
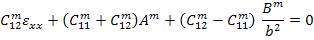 |
(7.189) |
The effective axial force can also be obtained by integrating the axial stresses in fibre and matrix over the cross sectional area as
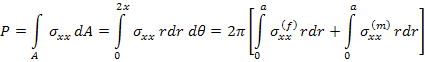 |
(7.190) |
Putting the expressions for 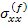 and and 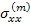 from Equation (7.185) and carrying out the integration we get from Equation (7.185) and carrying out the integration we get
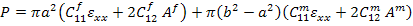 |
(7.191) |
The unknown constants 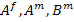 and and 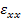 can be determined by solving Equations (7.180), (7.183), (7.189) and (7.191). The unknowns can be determined by solving Equations (7.180), (7.183), (7.189) and (7.191). The unknowns 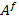 and and 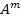 then can be used in Equation. (7.191) to calculate the axial force then can be used in Equation. (7.191) to calculate the axial force 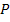 . .
The unknown constants 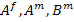 and and 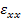 are given as are given as
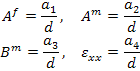 |
(7.192) |
where,
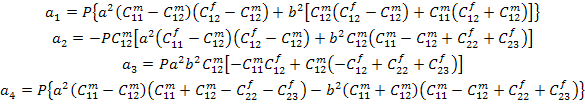 |
(7.193) |
|