| |
Effective Axial Modulus 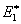 : :
The unit cell as shown in Figure 7.2 is used to compute the effective axial modulus 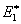 . It should be noted that the thickness of the unit cell is not important in this computation. Further, the cross sectional shapes are not considered in this calculation. However, the cross sectional areas are important in this calculation. The thicknesses of the fibre and matrix constituents are same in the unit cell. Hence, the areas of the constituents represent the volume fractions of the constituents. . It should be noted that the thickness of the unit cell is not important in this computation. Further, the cross sectional shapes are not considered in this calculation. However, the cross sectional areas are important in this calculation. The thicknesses of the fibre and matrix constituents are same in the unit cell. Hence, the areas of the constituents represent the volume fractions of the constituents.
In the calculation of effective axial modulus, it is assumed that the axial strain in the composite is uniform such that the axial strains in the fibers and matrix are identical. This assumption is justified by the fact that the fibre and the matrix in the unit cell are perfectly bonded. Hence, the elongation in the axial direction of the fibre and matrix will also be identical. Thus, the strains in the fibre and matrix can be given as
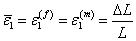 |
(7.14) |
where, 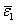 is the axial strain in the composite and is the axial strain in the composite and 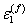 and and 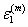 are the axial strains in fibre and matrix, respectively. Now, let are the axial strains in fibre and matrix, respectively. Now, let 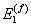 and and 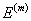 be the axial Young’s moduli of the fibre and matrix, respectively. We can give the axial stress in the fibre, be the axial Young’s moduli of the fibre and matrix, respectively. We can give the axial stress in the fibre, 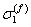 and matrix, and matrix, 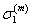 as as
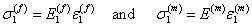 |
(7.15) |
Using the above equation and the cross section areas of the respective constituent in the unit cell, we can calculate the forces in them as
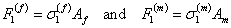 |
(7.16) |
|