Macroscopic Failure Theories:
In the following we will present some of the popular macroscopic failure theories used in design and analysis of composites.
In these theories we will use following quantities and symbols.
-
X denotes the ultimate normal stress magnitude in fibre direction (1-direction).
-
Y denotes the ultimate normal stress magnitude in in-plane transverse direction (2-direction).
-
Z denotes the ultimate normal stress magnitude in transverse direction (3-direction)
-
Subscript T and C denote tension and compression, respectively.
-
Q, R and S denote the ultimate shear stresses corresponding to 23, 13 and 12 planes.
We will see some definitions related to failure theories.
Strength Ratio (SR):
It is defined as the ratio of maximum load which can be applied such that a lamina does not fail to the actual load applied. Thus,
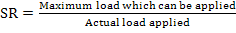 |
(6.1) |
This concept can be extended to any failure theory. The strength ratio gives the factor by which the actual applied load can be increased or decreased upto a lamina failure. For example, if 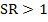 , it means that the lamina is safe and load applied can be increased by this factor and if , it means that the lamina is safe and load applied can be increased by this factor and if 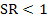 , it means that the lamina is unsafe and the load applied must be decreased by this factor. It is needless to say that when , it means that the lamina is unsafe and the load applied must be decreased by this factor. It is needless to say that when 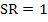 the condition corresponds to failure load. the condition corresponds to failure load.
Failure Envelope:
The failure envelope is a surface formed by various combinations of normal and shear stresses (or strains) that can be applied to a lamina just before it fails. Thus, any state of stress (or strain) which lies inside the envelope is safe whereas the one which lies on or outside the envelope is unsafe.
1. Maximum Stress Theory:
This theory is a direct extension of maximum normal stress theory proposed by Rankiene [1] and maximum stress theory proposed by Tresca [2] for homogeneous, isotropic materials. In this theory the three normal and three shear stress components are compared with corresponding ultimate stresses. A given normal stress is compared with corresponding positive and negative, that is tensile and compressive ultimate stresses. The magnitude of shear stress is compared with corresponding ultimate shear stress.
Thus, the maximum stress theory results in the following expression for the safe condition.
For normal stresses,
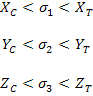 |
(6.2) |
For shear stresses,
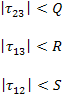 |
OR |
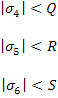 |
|
(6.3) |
Thus, according to this theory initiation of failure will correspond to one or more inequalities in Equations (6.2) and (6.3) become an equality. The maximum stress theory can be represented as intersecting planes in 3D stress space or intersecting lines in 2D stress space.
|