|
Governing Differential Equations for Classical Laminate Theory
The equilibrium equations for a laminate are
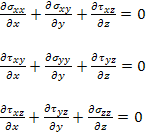 |
(5.133) |
In the laminate, in general, we consider that the transverse shear stresses are vanishing at the top and bottom of the laminate, that is 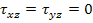 at at 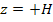 and and 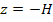 . Now, integrate Equation (5.133) with respect to z. The first two of the above equation give us . Now, integrate Equation (5.133) with respect to z. The first two of the above equation give us
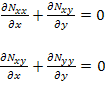 |
(5.134) |
The third of the Equation (5.133) gives
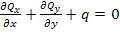 |
(5.135) |
where,
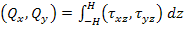 and and 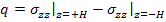 |
Now, multiply the first of Equation (5.133) with z and integrate with respect to z to get
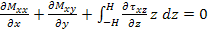 |
(5.136) |
Now, let us write
Now recalling that 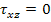 at at 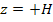 and and 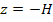 we can write for the third term in Equation (5.136) as we can write for the third term in Equation (5.136) as
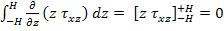 and and 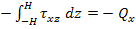 |
Thus, Equation (5.136) becomes
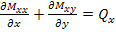 |
(5.137) |
Similarly, we can write
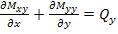 |
(5.138) |
Now putting Equation (5.137) and Equation (5.138) in Equation (5.135) we get
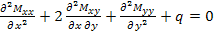 |
(5.139) |
Note that this equation is identical with the homogeneous plate theory. However, in these equations the definition of the resultants is different.
One can express the moment resultants in terms of A, B and D matrices and the derivatives of mid-plane displacements as given below.
Equation (5.137) can be written as
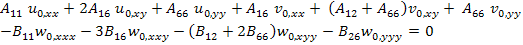 |
(5.140) |
Equation (5.138) becomes
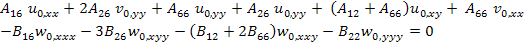 |
(5.141) |
And Equation (5.139) becomes
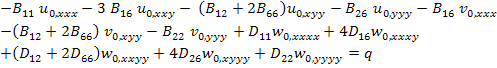 |
(5.142) |
|