|
Flexural Engineering Constants of a Laminate:
For a symmetric laminate, we have 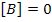 . Hence, from the second of Eq. (5.28) we write . Hence, from the second of Eq. (5.28) we write
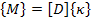 |
(5.87) |
Let us define the laminate average moments as 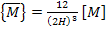
The inverse of this equation is written as
Writing this in expanded form
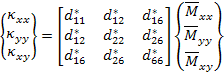 |
(5.88) |
Now the applied resultant moments be
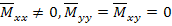 |
(5.89) |
Effective Flexural Longitudinal Young’s Modulus 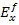 : :
Let us define the effective flexural Young’s modulus as
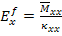 |
(5.90) |
Thus, using Equation (5.87) and Equation (5.88),
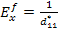 |
(5.91) |
Flexural Poisson’s Ratio 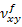 : :
Let us define flexural Poisson’s ratio as
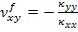 |
(5.92) |
Thus, from Equation (5. 87) and Equation (5.88),
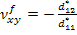 |
(5.93) |
In a similar way, one can show that the other flexural moduli can be given by following relations.
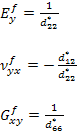 |
(5.94) |
Further, it can be shown that the reciprocal relation also holds true for flexural Poisson’s ratios as
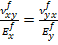 |
(5.95) |
|