Examples:
Example 2: Transform the stiffness and compliance matrix of Example 1 about axis 3 by an angle of
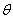 = 30°. = 30°.
Solution:
Approach 1: One can find the transformation matrices 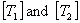 and do the matrix multiplication as given in Equation (3.73) for transformed stiffness matrix and then inverse this matrix or do the matrix multiplication as given in Equation (3.80) to get the transformed compliance matrix. The use of Equation (3.73) and Equation (3.80) is suggested because remembering and do the matrix multiplication as given in Equation (3.73) for transformed stiffness matrix and then inverse this matrix or do the matrix multiplication as given in Equation (3.80) to get the transformed compliance matrix. The use of Equation (3.73) and Equation (3.80) is suggested because remembering 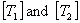 is not so difficult. Further, their inverse can be easily found with the help of Equation (3.74). is not so difficult. Further, their inverse can be easily found with the help of Equation (3.74).
For
Thus
Unit of all transformed stiffness coefficients is GPa.
Unit of all transformed compliance coefficients is 1/GPa.
Approach 2: You can write the expanded form for transformed stiffness and compliance coefficients in Equation (3.76) and Equation (3.82). However, the readers are suggested to use this approach only when they are confident of remembering these terms.
Example 3: The coefficients of moisture absorption for T300/5208 composite material are 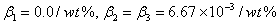 . Plot the variation these coefficients between . Plot the variation these coefficients between 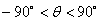 . .
Solution:
We have the expression for variation of the coefficients of moisture absorption as
where, 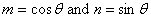 . We plot the above variation using a computer code. The final plot is shown in Figure 3.11. . We plot the above variation using a computer code. The final plot is shown in Figure 3.11.
| Figure 3.11: Variation of coefficients of moisture expansion with orientation of fibres |
|