Second Approach: Comparison of Constants
This can also be verified from the elastic constants expressed in terms of engineering constants like 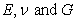 . Recall the constitutive equation for orthotropic material expressed in terms of engineering constants. For the transversely isotropic materials the following relations hold. . Recall the constitutive equation for orthotropic material expressed in terms of engineering constants. For the transversely isotropic materials the following relations hold.
When these relations are used in the constitutive equation for orthotropic material expressed in terms of engineering constants, the stiffness matrix relations in Equation (3.34) are verified.
Isotropic Bodies
If the function W remains unaltered in form under all possible changes to other rectangular Cartesian systems of axes, the body is said to be Isotropic. In this case, W is a function of the strain invariants. Alternatively, from the previous section, W must be unaltered in form under the transformations
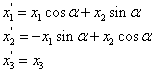 |
(3.35) |
and
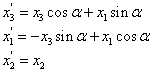 |
(3.36) |
In other words, W when expressed in terms of 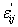 must be obtained from Equation (3.33) simply by replacing must be obtained from Equation (3.33) simply by replacing 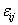 by by 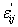 . By analogy with the previous section it is seen that for this to be true under the transformation Equation (3.35). We can write . By analogy with the previous section it is seen that for this to be true under the transformation Equation (3.35). We can write
And the transformed strains are given as
 |
(3.37) |
Thus, for any angle α,
 |
(3.38) |
and therefore, W must reduce to the form
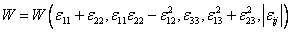 |
(3.39) |
Then, for W to be invariant we must have
Now, let us write the left hand side of above equation using the 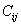 matrix as given in Equation (3.34) and engineering shear strains. In the following we do some rearrangement as matrix as given in Equation (3.34) and engineering shear strains. In the following we do some rearrangement as
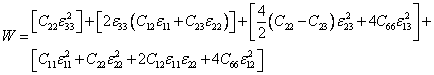 |
(3.40) |
Similarly, we can write the right hand side of the previous equation using rotated strain components. Now, for W to be invariant it must be of the form as in Equation (3.39)
- From the second bracket, if we propose
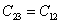 , then we can satisfy the first of Equation (3.38). , then we can satisfy the first of Equation (3.38).
- From the third bracket, third of Equation (3.38) holds true when
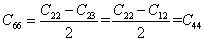 . .
- The fourth bracket is manipulated as follows:
Thus, to satisfy the second of Equation (3.38) we must have 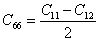 . Further, we should have . Further, we should have 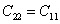 . From our observation in 2, we can write . From our observation in 2, we can write 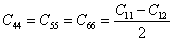 . .
It follows automatically that W is unaltered in form under the transformation in Equation (3.36).
Thus, the stiffness matrix for isotropic material becomes as
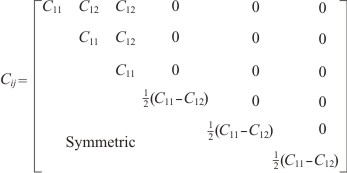 |
(3.41) |
Thus, for an isotropic material there are only two independent elastic constants. It can be verified that W is unaltered in form under all possible changes to other rectangular coordinate systems, that is, it is the same function of  as it is of as it is of 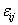 when when 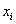 is changed to is changed to 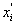 . . |