|
Let 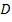 be the average diameter of the fibres, be the average diameter of the fibres, 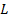 be the length of the fibres and be the length of the fibres and 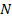 be the number of fibres for a given volume of fibres in a composite. Then the surface area available for load transfer is be the number of fibres for a given volume of fibres in a composite. Then the surface area available for load transfer is
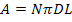 |
(1.1) |
The volume of these fibres in a composite is
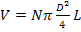 |
(1.2) |
Now, let us replace the fibres with a smaller average diameter of 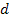 such that the volume of the fibres is unchanged. Then the number of fibres required to maintain the same fibre volume is such that the volume of the fibres is unchanged. Then the number of fibres required to maintain the same fibre volume is
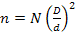 |
(1.3) |
The new surface area between fibre and matrix is
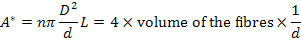 |
(1.4) |
Thus, for a given volume of fibres in a composite, the area between fibre and matrix is inversely proportional to the average diameter of the fibres.
c) The fibres should be flexible so that they can be bent easily without breaking. This property of the fibres is very important for woven composites. In woven composites the flexibility of fibres plays an important role. Ultra thin composites are used in deployable structures.
The flexibility is simply the inverse of the bending stiffness. From mechanics of solids study the bending stiffness is EI, where 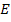 is Young’s modulus of the material and is Young’s modulus of the material and 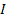 is the second moment of area of the cross section of the fibre. For a cylindrical fibre, the second moment of area is is the second moment of area of the cross section of the fibre. For a cylindrical fibre, the second moment of area is
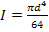 |
(1.5) |
Thus,
Flexibility 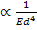 |
(1.6) |
Thus, from the above equation it is clear that if a fibre is thin, i.e. small in diameter, it is more flexible.
|